ViennaFEM

Content

Example: Poisson Equation

The essential steps in the numerical solution of the Poisson equation as considered in the previous example using ViennFEM is shown here. Aside from a few technical type definitions, all user code is shown. Moreover, the code is essentially unchanged for 1d, 2d, and 3d. At the end of the page you will know all the high-level code required for solving the Poisson equation on an interconnect and be able reproduce the following result:

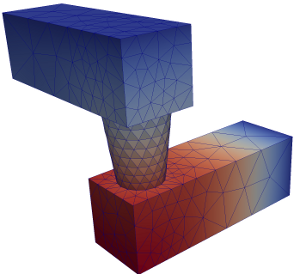
The first step is to read the mesh from file to a ViennaGrid domain object:

Step 1: Read the mesh

DomainType my_domain;
viennagrid::io::netgen_reader my_reader;
my_reader(my_domain, "../examples/data/sshape3d-pimped.mesh");

Here, a sample mesh included in the release package is used.

The next step is to supply Dirichlet boundary conditions to the boundary vertices. It is possible to use separate boundary conditions for many different PDEs on the same mesh. For demonstration purposes the simplest form is considered:

Step 2: Write boundary conditions to the domain

  VertexContainer vertices = viennagrid::ncells<0>(my_domain);
  for (VertexIterator vit = vertices.begin();
      vit != vertices.end();
      ++vit)
  {
    //Dirichlet conditions at vertices with z == 3.0 or y == 3.0
    if (vit->point()[2] == 3.0 || vit->point()[1] == 3.0 )
      viennafem::set_dirichlet_boundary(*vit, 0.0);
  }

Next, the Poisson equation is set up and the linear system is instantiated. 'MatrixType' and 'VectorType' are generic types, in our case from Boost.uBLAS.

Instantiating Poisson equation and the linear system

viennamath::function_symbol u;
viennamath::equation poisson_eq = viennamath::make_equation( viennamath::laplace(u), -1);
 
MatrixType system_matrix;
VectorType load_vector;

Now everything is ready for the assembly. For that purpose an assembly functor is instantiated and called:

FEM assembly

viennafem::pde_assembler fem_assembler;
 
fem_assembler(viennafem::make_linear_pde_system(poisson_eq, u),
              my_domain,
              system_matrix,
              load_vector);

The assembled system is now solved using the conjugate gradient solver provided with ViennaCL and then written to a VTK file for further processing in e.g. ParaView.

Solving the system, writing result to VTK

VectorType pde_result = viennacl::linalg::solve(system_matrix,
                                                load_vector,
                                                viennacl::linalg::cg_tag());
 
viennafem::io::write_solution_to_VTK_file(pde_result, "sshape_3d", my_domain);